The Wente torus

The image on the top-left of our home page is a computer-generated view of an amazing three-lobed surface discovered in 1984 by Dr. Henry Wente of the UT Mathematics Department. (The two images at the bottom of this page are of Wente tori which have been "lobotomized" to reveal some of the inner structure.)

It is not at all obvious (even in the higher resolution images from which these picture was taken) but topologically, this surface is equivalent to a standard torus; if it were made of an imaginary stretchable material which could be pushed through itself, it could be deformed (without cutting or tearing) into the surface of a doughnut or inner tube.

What makes this immersion of the torus remarkable is that its mean curvature is the same at every point.

Constant mean curvature is a property common to all shapes assumed by stable soap bubbles or films. However, until Wente's discovery, with the single exception of the sphere, all known examples of compact surfaces of constant mean curvature had one or more edges or boundary curves (i.e. they did not "close up").

It was a very plausible and long-standing conjecture (which can be traced back to the early 19th century) that the sphere was the only example of such a surface. As it happens, the torus (a one-holed doughnut) is not the only exception: in fact, subsequent to Wente's work, examples of boundaryless, compact constant mean curvature surfaces were constructed in every genus (i.e. with an arbitrary number of "holes").

Also subsequent to Wente's work, all toral soap bubbles were classified via methods from soliton theory. Numerous researchers are still studying the ramifications of Wente's breakthrough.

It is notable that, despite the fact that high-speed computers have become a powerful tool for formulating and investigating conjectures in this area (and the complex structure of Wente's surface would be very difficult to display without them), computers played no role in Wente's proof that his counterexample existed.

A full size version of the image used in the logo (along with other related images) can be found on the web page of Ivan Sterling. The Mathematical Sciences Research Institute at Berkeley has a Wente torus page with some beautiful pictures. There are also many other interesting images on their Scientific Graphics Project page.

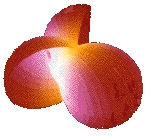
Wente's paper appeared in the Pacific Journal of Mathematics, Vol 121, No.1 (January 1986), pp. 193-243. A non-technical account (with some computer-generated images) of this and other recent advances in the geometry of surfaces (and other areas of mathematics) can be found in Ivars Peterson's book, "The Mathematical Tourist" (Freeman).

A former Ph.D. student at UT, Andreia Mahler, has a picture gallery of surfaces from her thesis displayed on her personal web page.